Служу я украшением стола (© ?)
Блажен в златом кругу вельмож
Пиит, внимаемый царями.
Владея смехом и слезами,
Приправя горькой правдой ложь,
Он вкус притупленный щекотит
И к славе спесь бояр охотит,
Он украшает их пиры,
И внемлет умные хвалы.
Меж тем, за тяжкими дверями,
Теснясь у чёрного крыльца,
Народ, гоняемый слугами,
Поодаль слушает певца.
Автор: Александр Пушкин
Блажен в златом кругу вельмож...
Бесконечность -- понятие с которым мы сталкиваемся буквально с того момента, когда мы учимся считать. Все наверное пытались в своё время придумать "самое большое число" (и начинались перечисления вида "тысяча, миллион, миллиард, квадриллион, кто-то даже до гугла доходил может быть). Но всегда оказывалось, что чтобы ты не придумал, всегда можно прибавить единичку и получить ещё больше! Так мы понимаем, что целых чисел бесконечно много. Потом разных бесконечностей становится больше -- например в геометрии у нас возникает понятие "точки на плоскости" и мы конечно же понимаем, что точек у нас бесконечно много. Возникает вопрос -- а как сравнивать эти бесконечности (в моём детстве я помню был какой-то спор меня с моим тогдашним приятелем, и мы мерились бесконечностями -- типа "А моё заклинание в бесконечное количество раз сильнее твоего", "а моё в бесконечность-в-квадрате больше!"). И действительно часто возникает ощущение, что одна бесконечность больше другой.
Например, возьмём целые числа и выберем из них положительные (т.е. натуральные). Видно, что мы выбрали половину всех чисел. Получается, что целых чисел в два раза больше! Очевидно? Очевидно, только неверно. И для того чтобы понять почему это не так, давайте разберёмся вообще с тем, что означает для бесконечностей "равно", "больше" или "меньше".
Давайте представим себе, что есть в нашем мире большой трактир, куда пришли гномы. И вот садятся они за большой стол и заказывают себе пива. Вопрос -- как определить, что трактирщик правильно подсчитал гномов и принёс правильное количество кружек пива? Самый очевидный вариант -- каждому гному досталось по кружке и никаких лишних кружек не осталось. Т.е. на самом деле что мы сделали -- мы сказали, что каждой кружке соответствует (ровно один) гном и каждому гному соответствует (ровно одна) кружка (гномы любят справедливость и поэтому нещадно дубасят того кто получил случайно больше). Выглядит как логичный способ определить равенство количества элементов. Аналогично легко понять что означает что пива меньше чем гномов -- как бы ты честно не раздавал кружки, всегда найдётся гном без пива.
Предположим теперь что у нас пришло бесконечное количество гномов и уселось за бесконечно длинный в обе стороны стол, а проклятый трактирщик взял, всё напутал и поставил бесконечное количество пива только правой половине гномов:
Всё уже идет к тому, что сейчас начнётся массовая драка за пиво, но, к счастью, внезапно появляется мудрый волшебник и говорит: "Постойте друзья! Сейчас я сотворю магию и каждому гному достанется по пиву". И делает следующую процедуру -- первое пиво передвигает центральному гному №0. Второе пиво даёт гному №1, третье пиво -- гному № -1, четвертое -- №2, пятое -- № -2, 6е -- №3, и т.д. Т.е. пиво с чётными номерами он последовательно даёт гномам справа, а с нечётными -- слева. Что в итоге получится? Пива очевидно осталось столько же -- мы только передвигали кружки между гномами, но в конце у каждого гнома оказалась по одной кружке!
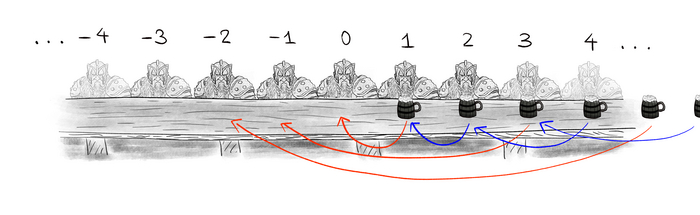
Что же это получается? Получается что половина бесконечности равна ей всей. Это один из "парадоксов" который возникает с бесконечностями -- иногда оказывается что в части бесконечности такое же количество элементов, что и во всей.
Автор: TeoretikX
Бесконечный рассказ о бесконечности -- гномы и пиво. Избранное.